개발자 블로그
프로그래머스 - 소수 찾기 본문
문제 설명
1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution을 만들어 보세요.
소수는 1과 자기 자신으로만 나누어지는 수를 의미합니다.
(1은 소수가 아닙니다.)
제한 조건
- n은 2이상 1000000이하의 자연수입니다.
입출력 예
nresult| 10 | 4 |
| 5 | 3 |
입출력 예 설명
입출력 예 #1
1부터 10 사이의 소수는 [2,3,5,7] 4개가 존재하므로 4를 반환
입출력 예 #2
1부터 5 사이의 소수는 [2,3,5] 3개가 존재하므로 3를 반환
나의 풀이
def decimal(n):
if n == 1:
return False
for i in range(2, int(n**0.5)+1):
if n % i == 0:
return False
return True
def solution(n):
answer = 0
for i in range(1, n+1):
if decimal(i):
answer += 1
return answer
* 소수를 구하는 함수를 구했다. 소수를 확인하는 함수의 알고리즘은 제곱근까지만 수의 약수가 있는지만 확인하면 된다.
소수를 구하는 또 다른 풀이를 보며 비교해보자! 함께 알고리즘 공부를 하고 있는 재명님의 풀이다!
소수 판별하는 에라토스테네스의 체
def solution(n):
table = [False, False]+[True]*(n-1) # 0부터 해당하는 값까지 약수인지 True, False로 테이블 생성
m = int(n ** 0.5)
for i in range(2, m+1): # 해당 수가 소수인지 판별하기 위해 제곱근까지만 확인하면 됨.
if table[i]: # 해당 값이 True이면,
for j in range(2*i, n+1, i): # 해당 수의 배수들만 찾기 위해, (i+i, n+1, i) i이후에 i의 배수들을 False로 판정, 괄호 안 3번 째 i는 i만큼 건너띄라는 말로 i의 배수를 확인하는 거라 볼 수 있다.
table[j] = False
count = 0
for i in range(2,n+1):
if table[i] == True:
count += 1
return count
에라토스테네스의 체 : 범위에서 합성수를 지우는 방식으로 소수를 찾는 방법. 1. 1은 제거 2. 지워지지 않은 수 중 제일 작은 2를 소수로 채택하고, 나머지 2의 배수를 모두 지운다. 3. 지워지지 않은 수 중 제일 작은 3을 소수로 채택하고, 나머지 3의 배수를 모두 지운다. 4. 지워지지 않은 수 중 제일 작은 5를 소수로 채택하고, 나머지 5의 배수를 모두 지운다. 5. (반복)
고대 그리스의 수학자 에라토스테네스가 만들어 낸 소수를 찾는 방법. 이 방법은 마치 체로 치듯이 수를 걸러낸다고 하여 '에라토스테네스의 체'라고 부른다.
아래 그림으로 알고리즘이 진행되는 모습을 육안으로 확인할 수 있다.
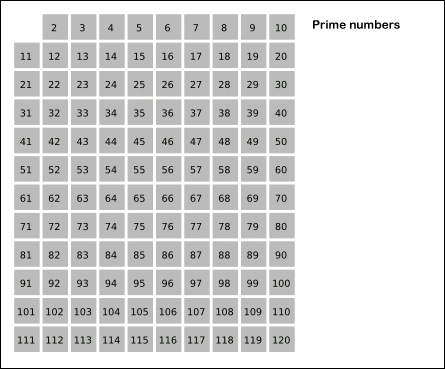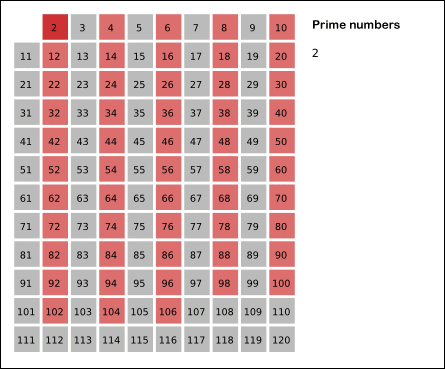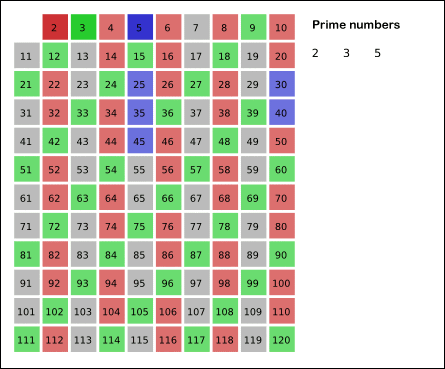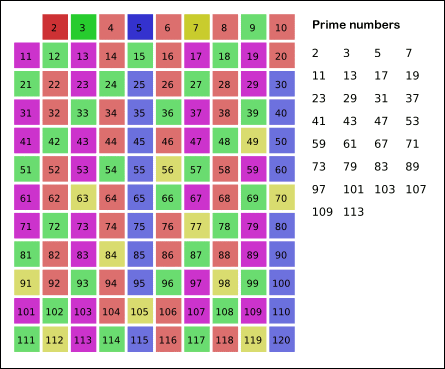
임의의 자연수 n이 있으면 그 이하의 소수들을 전부 찾아내는 데 있어서 최적화된 알고리즘이라고 할 수 있다. 기원전 200년대부터 쓴 검증된 로직이다.
풀이 비교
풀이 1과 풀이 2를 비교하자면, 범위에 숫자들의 소수 판별은 에라토스테네스의 체를 활용하여 이중 for문 안에 들어갈 수 범위를 줄여나가는 것이 훨씬 효율적이라고 본다. -> 배수를 다 false라고 바꾸고 if문으로 true만 확인하여 들어가니까! 모든 수가 이중으로 들어갈 필요가 없음. 실제 테스트 통과 시간이 훨씬 줄어든 것을 확인했다!
풀이 1에서는 모든 수를 소수인지 판별을 했다면, 에라토스테네스의 체는 해당하는 수의 배수를 모두 지워나가는 방식으로 범위의 숫자들의 소수를 판별하는 문제에서는 시간복잡도가 상위에 있을 것이다.
'알고리즘 > 프로그래머스' 카테고리의 다른 글
| 프로그래머스 - '수박수박수박수?' (0) | 2022.04.27 |
|---|---|
| 프로그래머스 - 약수의 합 (0) | 2022.04.27 |
| 프로그래머스 - 서울에서 김서방 찾기 (0) | 2022.04.26 |
| 프로그래머스 - 문자열 내 마음대로 정렬하기 (0) | 2022.04.26 |
| 프로그래머스 - 2018카카오 블라인드 채용 [1차] 다트 게임 (0) | 2022.04.25 |
